This post was published in french under Etude du comportement de treillis par la méthode des éléments finis.

Je tiens à remercier Pierre et Mathieu pour la rédaction de ce document. Merci les gars.

Ce tutorial consiste à présenter et caractériser les treillis c’est-à-dire déterminer les efforts intérieurs de ce type de système et en déduire les déplacements des différents nœuds. Afin de résoudre ce problème, on utilisera la méthode des éléments finis qui sera en partie expliquée dans ce rapport. Par la suite, pour appliquer cette méthode, on prendra comme exemple la poutre des amphithéâtres Pasteur. Tous les calculs matriciels ont été effectués grâce au logiciel Matlab.

Présentation d’un modèle : le ressort

Propriétés d’un ressort simple

Tout le monde a étudié l’équilibre d’un ressort élastique caractérisé par sa rigidité k. Cette constante intervient en effet dans le calcul de la force de rappel : F = k x d , où d est la variation relative de longueur du ressort. Cette expression va par la suite être généralisée à une structure en treillis.

Matrice de rigidité d’un ressort élastique

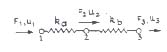
Considérons maintenant le cas d’un ressort soumis à deux forces axiales s’appliquant sur ses extrémités.

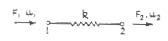
L’équilibre pour chaque nœud impose :

où , , et sont respectivement les forces et les déplacements pour chaque nœud.

Ces équations peuvent être écrites sous forme matricielle de la façon suivante:

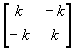
La nouvelle matrice de dimension 2 ainsi créée s’appelle matrice de rigidité du ressort.

Cas d’un système de ressorts

Cette nouvelle étape consiste à montrer comment les matrices de rigidité peuvent être combinées pour former la matrice de rigidité d’une structure comportant plusieurs ressorts. Tout d’abord, en procédant de la même manière que ci-dessus, on va chercher à obtenir la matrice de rigidité d’un système de deux ressorts.

On aboutit aux équations suivantes :

L’écriture de ces équations sous forme matricielle donne :

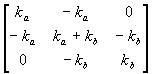
Pour chaque élément constitutif de la structure, s’écrit :

Elément 1 :

Elément 2 :

Bien que les deux matrices soient du même ordre, elles ne peuvent être ajoutées directement puisqu'elles se rapportent à des ensembles de déplacements différents. Cependant, en insérant des lignes et des colonnes de zéros, toutes deux peuvent être développées de telle façon qu'elles se rapportent aux mêmes déplacements , et .

Ka=

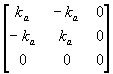
Kb=

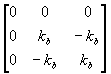
En sommant ces deux matrices, on obtient bien la matrice de rigidité du système de ressorts.

Hypothèses simplificatrices

Forces ponctuelles

On suppose dans notre modèle que toutes les forces s’appliquent ponctuellement uniquement au niveau des nœuds. De plus, comme pour les ressorts, On ne considère que les efforts axiaux s’appliquant sur chaque élément du treillis.

Propriétés des nœuds

Tous les nœuds sont considérés comme des liaisons charnières pour lesquelles les frottements seront négligés. De plus, ces liaisons sont dans la plan et ne possèdent donc que deux degrés de liberté.

Poids propre des éléments

Le poids propre de chacun des éléments, s’il n’est pas négligeable par rapport aux efforts exercés sur le treillis, sera pris en compte comme une force s’exerçant au niveau des deux extrémités de l’élément.

Méthode de résolution

Calcul des matrices de rigidité de chaque élément

Nous allons maintenant montrer la marche à suivre complète sur un exemple très simple. Cette démarche est bien sûr celle qu’il convient d’utiliser pour n’importe quel treillis. Considérons donc l’armature de poutres représentée ci-dessous :

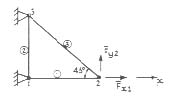
Puisqu’il y a trois nœuds ayant deux degrés de liberté chacun, les vecteurs des charges appliquées et des déplacements contiennent chacun six termes dans le repère absolu :

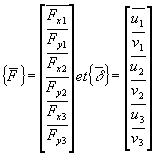
Ensuite, on calcule la matrice de rigidité de chaque élément. Pour cela, il faut déterminer f , angle entre l’axe des abscisses et l’élément. Ainsi, pour notre exemple, on a :

phi cos (phi) sin (phi)
0° 1 0
90° 0 1
135° -  

On forme les matrices de rigidité qui est de la forme suivante :

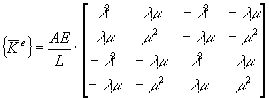
où:

  • A représente la section,
  • E le module d’Young,
  • L la longueur de l’élément.
  • Le terme AE/L correspond au k du ressort.

Assemblage de la matrice de rigidité

On additionne maintenant les matrices de rigidité déterminées précédemment afin d’obtenir la matrice de rigidité de la structure. Pour cela, on peut appliquer la méthode suivante : on divise la matrice de chaque élément en quatre et on “place” chacune de ces sous-matrices respectivement à l’intersection des lignes et des colonnes de la matrice de rigidité du système, correspondant aux deux nœuds extrémités de l’élément. Pour notre exemple, l’expression de celle-ci est :

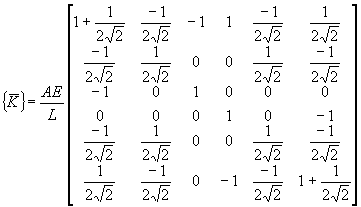
Application des conditions aux limites

En remarquant que les nœuds 1 et 3 sont fixes, l’équation matricielle gouvernant la structure peut être simplifiée. Le vecteur déplacement s’écrit ici :

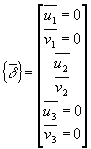
Calcul des déplacements

Calcul des inconnues dans l’exemple du triangle

Aux nœuds 1 et 3, où (déplacements imposés), il n'est pas possible d'imposer également les efforts et . Les valeurs de ceux-ci résulteront en fait de l'effort appliqué . On dit que et sont des réactions d'appui. Ces réactions apparaissent bien comme des inconnues supplémentaires au même titre que les déplacements. Les modalités du calcul sont les suivantes.

On résout d’abord le système d’équations dans lequel n’apparaissent que les degrés de liberté (d.d.l.) non nuls et le chargement extérieur imposé.

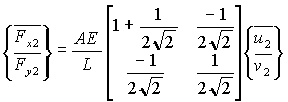
On remarque que pour obtenir ce système, il suffit de supprimer, dans la matrice de raideur de la structure, la ligne et la colonne correspondant aux d.d.l. nuls.

En inversant le système, on obtient :

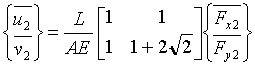
On calcule ensuite les réactions d'appui et au moyen de la relation suivante :

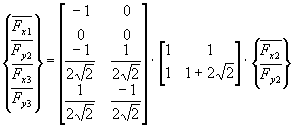
Généralisation

Lorsque la structure est convenablement appuyée (les mouvements d'ensembles ne sont pas possibles), un certain nombre de d.d.l. sont bloqués. Désignons par ces d.d.l. ( ). Les d.d.l. demeurés libres sont notés . Pour la structure complète, on fait ainsi la distinction :

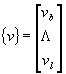
Le système d'équations complet ( ) peut être alors réarrangé de la façon suivante :

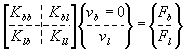
conduisant aux deux sous-systèmes :

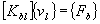
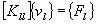
La procédure de résolution est ensuite identique à celle décrite dans la première partie.

Application : la poutre de l’amphithéâtre Pasteur

Nous allons maintenant appliqué cette méthode à la poutre de notre cher amphithéâtre Pasteur. Pour cela, nous avons discrétisé le treillis en 39 éléments ce qui représente 21 nœuds, la dimension de la matrice de rigidité du système est ainsi de 42.

On considère que la section est la même pour tous les éléments : 0,2 m2, soit un diamètre de 50 cm.

Les forces sont appliquées aux points nodaux de la barre supérieure et sont estimées à 10 kN chacune.

Le module d’Young utilisé est celui de l’acier (E=210 GPa).

La résolution de ce problème est fourni en annexe ainsi que les scripts Matlab de notre programme.

Conclusion

Ainsi la méthode des éléments finis nous a permis d’approximer le calcul d’une structure complexe.

Pour un gain de performance dans le calcul de la matrice de rigidité globale, il faudrait optimiser la numérotation des nœuds pour obtenir des matrices bandes et utiliser la propriété de symétrie de la matrice.

Nous avons soulevé ici qu’une partie du champ d’application de la théorie des éléments finis. En effet, qu’en est-il de la matrice de rigidité pour des éléments surfaciques ou volumiques ? Comment prendre en compte les efforts de flexions et de torsion qui existe dans la réalité ?

Bibliographie

  • K.C. Rockey, H.R. Evans, D.W. Griffiths et D.A. Nethercot, Introduction à la méthode des éléments finis, édition Eyrolles, Paris.
  • A. Picard, Analyse des structures, édition Masson, Paris.
  • D. Gay et J. Gambelin, Une approche simple du calcul des structures par la méthode des éléments finis, éditions Hermès, Paris.